Статистическая обработка результатов анализа
В силу особенности химического анализа (отсутствие истинного значения величины, малые выборки) значимыми являются не столько сами результаты анализа, сколько их характеристики:
- Точность - качество измерений, отражающее близость их результатов к истинному значению измеряемой величины.
- Воспроизводимость степень близости друг к другу независимых результатов анализов, полученных одним и тем же методом, на идентичных объектах, в разных лабораториях, разными операторами, с использованием различного оборудования.
- Сходимость - близость результатов измерений приведённых в одинаковых условиях.
- Правильность - качество измерений, отражающее близость к нулю систематических погрешностей.
Для оценки данных характеристик используют методы математической статистики, разработанные для малых выборок. В итоге результаты представляют в виде некоторого интервала в который с определённой вероятностью входит действительное значение величины. При использовании математического аппарата для обработки оперируют понятиями:
- Выборка – реальное число вариант n которое имеет исследователь.
- Математическое ожидание (μ) величины – предел к которому стремится среднее арифметическое выборки при бесконечном увеличении объёма выборки.
- Среднее арифметическое вариант:
- Дисперсия
выборочная (S2) – величина характеризующая отклонение вариант
относительно среднего.
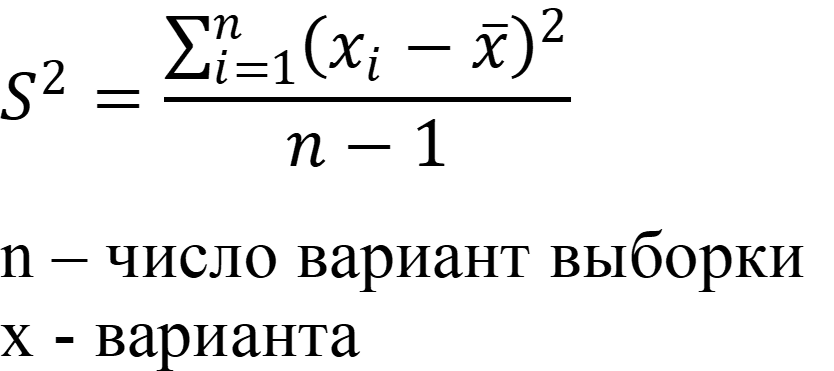
- Стандартное отклонение
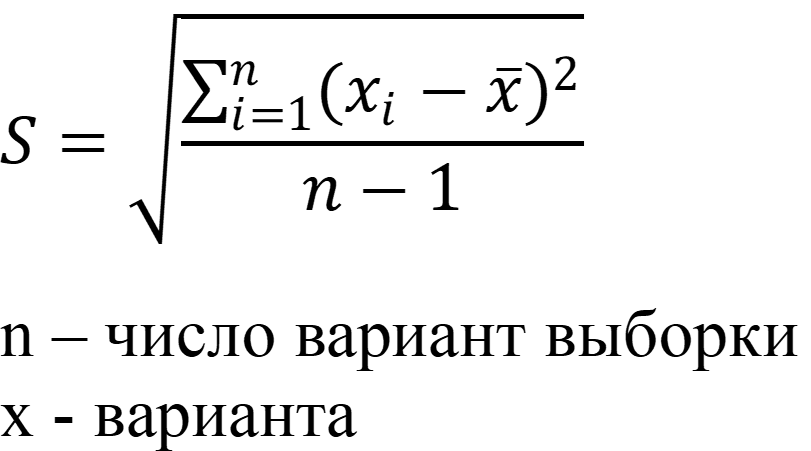
- Относительное стандартное
отклонение

- Распределение Стьюдента
(распределение) – распределение нормированной случайной величины t.

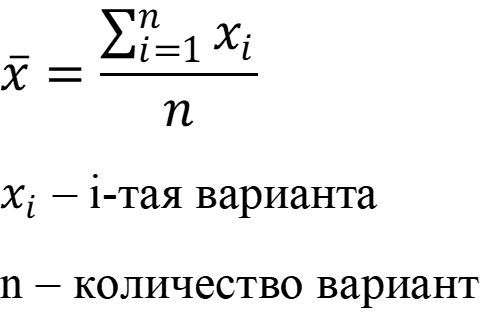
При статистической обработке данных предполагается, что варианты выборки случайные величины и распределены по нормальному закону.
Требования к выборке:
- Систематические погрешности при анализе выявлены и устранены или переведены в разряд случайных
- Выявлены и устранены грубые промахи
- Отсутствие дрейфа данных
В общем случае математическая обработка результатов анализа включает в себя стадии:
- Определение и исключение грубых промахов
- Выявление дрейфа данных
- Расчёт среднего арифметического вариант
- Расчёт стандартного отклонения выборки
- Расчёт доверительного интервала
- Расчёт погрешности анализа

