АНАЛИТИЧЕСКАЯ ХИМИЯ

Задача №1:

Из двух растворов с концентрацией некоторого вещества 10 и 27 % необходимо приготовить 230 г раствора с концентрацией 17 %. Сколько грамм каждого из исходных растворов необходимо взять.

Дано:

ω₁ = 10 %
ω₂ = 27 %
ω_x = 17 %
m_x = 230 г
m₁ - ?
m₂ - ?

Решение:

Если раствор получают смешиванием двух других растворов, один из которых имеет большую концентрацию, а другой - меньшую, то массу исходных растворов можно определить, пользуясь правилом разбавления («правилом креста»), которое для растворов определенной процентной концентрации гласит: массы смешиваемых растворов обратно пропорциональны разностям процентных концентраций смешиваемых и получаемого растворов. Это правило выражают схемой:

При использовании этого правила следует помнить о том, что расчёт ведётся для масс растворов и если исходные данные в объёмах или необходимо найти объём, то необходимо использование справочных данных о плотностях растворов!!!

Применим правило для нашего случая:

Масса одной части:

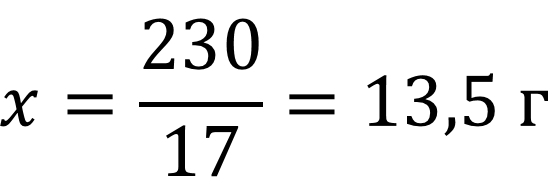
m₁ = 10 * 13,5 = 135 г

m₂ = 7 * 13,5 = 95 г

Для проверки рассчитаем сумму:

m₁ + m₂ = 135 + 95 = 230 г

Ответ: m₁ = 135 г; m₂ = 95 г.

Задача №2:

Смешали два раствора с массами по 100 г. Рассчитать конечную концентрацию, если исходные равны 11 и 30 %.

Дано:

ω₁ = 11 %
ω₂ = 30 %
m_1,2 = 100 г
ω_x - ?

Решение:

«Правило креста» - равносильно во всех направлениях и каждый элемент цепочки можно рассчитать, имея остальные данные, для данного случая:

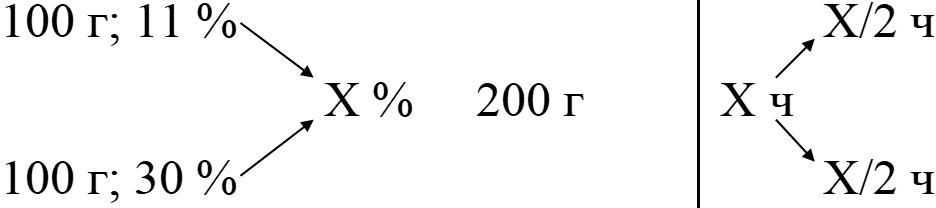
Соответственно:

ω_x - ω_меньш. = X/2

ω_больш. - ω_х = X/2

Приравнивая:

ω_x - ω_меньш. = ω_больш. - ω_х

Из полученного уравнения:

ω_x - 11 = 30 - ω_х

ω_x = 20,5

Ответ: ω_х = 20,5 %