АНАЛИТИЧЕСКАЯ ХИМИЯ

Грубая погрешность, промах - погрешность результата отдельного измерения, входящего в ряд измерений, которая для данных условий резко отличается от остальных результатов этого ряда.

Вопрос о том, содержит ли результат наблюдений промах, решается общими методами проверки статистических гипотез. Проверяемая гипотеза состоит в утверждении, что результат наблюдения X, не содержит грубой погрешности, т.е. является одним из значений измеряемой величины. Пользуясь определенными статистическими критериями, пытаются опровергнуть выдвинутую гипотезу. Если это удается, то результат наблюдений рассматривают как содержащий грубую погрешность и его исключают.

Одним из критериев для проверки на грубые промахи является Q – тест.

Для проверки на наличие грубых промахов проводят упорядочивание по величине вариант с последующей проверкой крайних членов выборки. Формулы для вычислений:

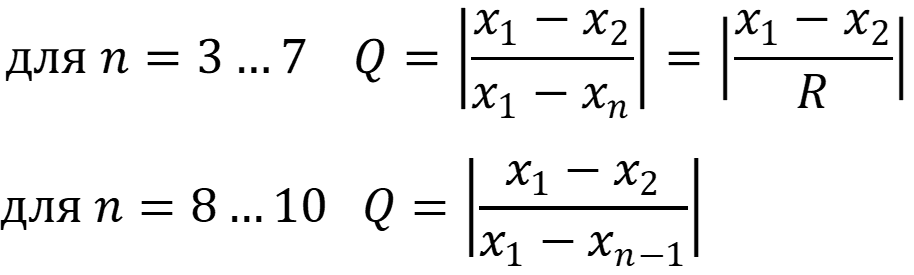
Найденное значение Q для данной варианты X сравнивается с табличным значением Q_табл. для заданной степени вероятности. При отсутствии данных Р = 0,95.

Если Q > Q_табл., то X можно считать грубым промахом. Если Q ≤ Q_табл., то результат не отбрасывают.

Задача №1:

При определении серы в нефти методом потенциометрического титрования были получены следующие результаты (% масс): 3,4; 3,7; 3,5; 3,6; 4,2; 3,5. Проверить данные на наличие грубых промахов.

Решение:

Расположим варианты выборки в порядке убывания величины: 4,2; 3,7; 3,6; 3,5; 3,5; 3,4. Сомнительной по величине вариантой является 4,2. Проверим по Q – тесту:

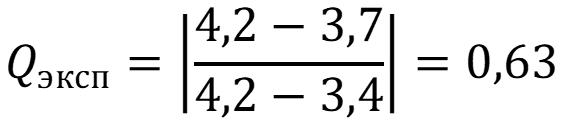
Q_табл. при Р = 0,95 равно 0,56

Ответ: Q_эксп > Q_табл. – варианта 4,2 является грубым промахом.

Вариантом для более объёмных выборок является критерий Романовского (10 < n < 20)

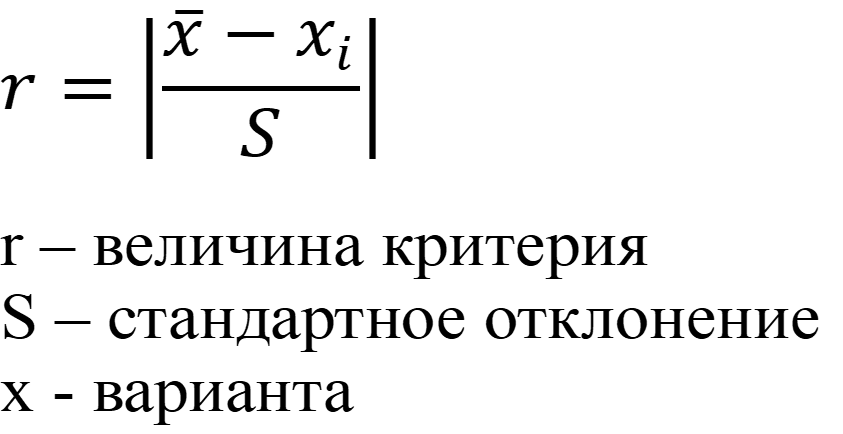
Найденное значение r для данной варианты X сравнивается с табличным значением r_табл. для заданной степени вероятности.

При отсутствии данных Р = 0,95.

Если r > r_табл., то можно считать грубым промахом. Если r ≤ r_табл., то результат не отбрасывают.

Задача №2:

При определении содержания аренов в нефти хроматографическим методом были получены следующие результаты (% масс.): 17; 18; 20; 17; 23; 25; 27; 19; 15; 17; 18; 22. Проверить данные на наличие грубых промахов.

Решение:

Расположим варианты выборки в порядке убывания величины: 27; 24; 23; 22; 20; 19; 18; 18; 17; 17; 17; 15.

Сомнительными по величине вариантами являются 27 и 15.

Рассчитаем среднее арифметическое для вариант без учёта подозрительных:

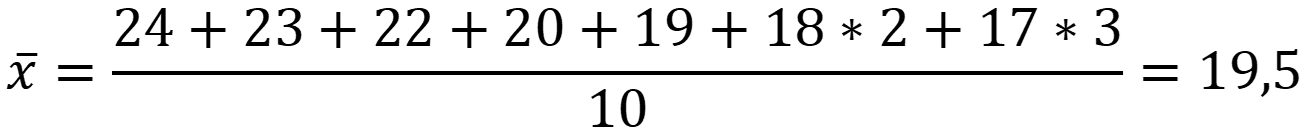
Рассчитаем стандартное отклонение для выборки:

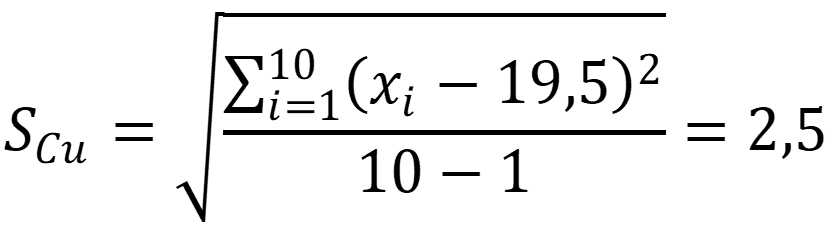
Рассчитаем экспериментальное значение r для каждой сомнительной варианты:

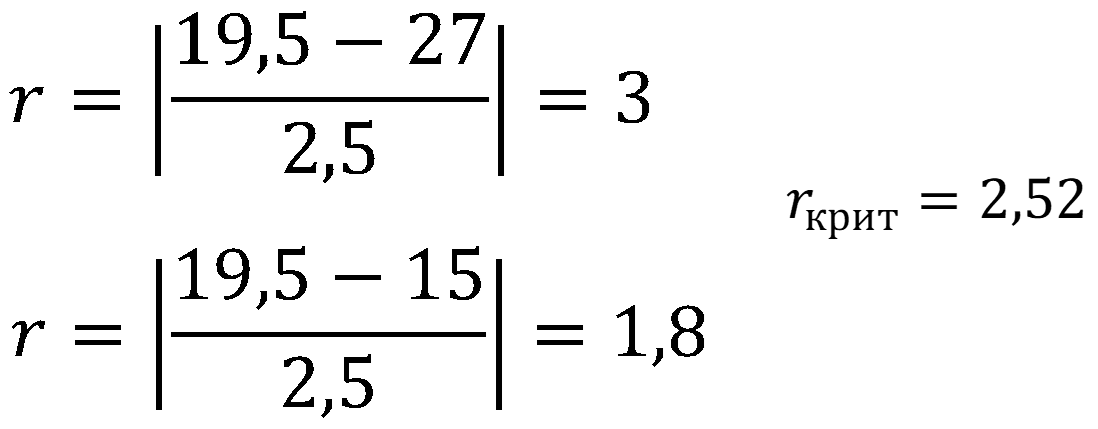
Ответ: варианта 27 является грубой погрешностью так как экспериментальное значение критерия больше критического.

Видео можно посмотреть тут.