Оценка разброса данных
Стандартное отклонение - параметр выборки, характеризующий случайную ошибку эксперимента, мера разброса отдельных измерений относительно среднего арифметического вариант.
Рассчитывается по формуле:
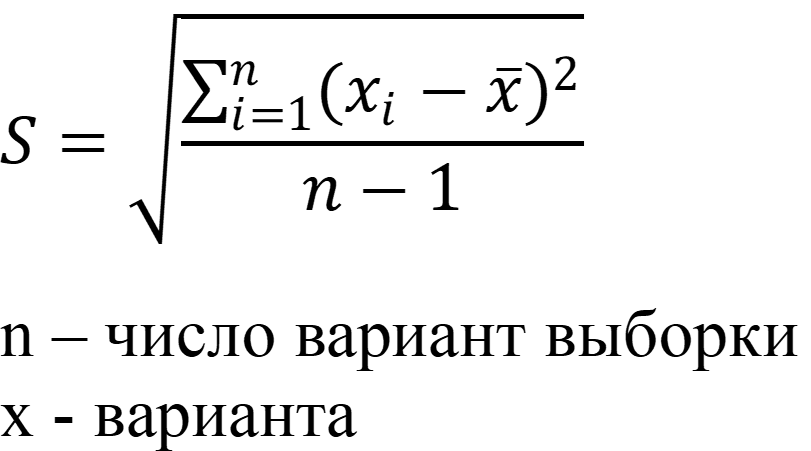
Задача №1:
При определении содержания меркаптановой серы в нефти получили ряд данных в % масс.: 1,07; 1,11; 1,13; 1,09; 1,17. Определить среднее значение содержания серы и стандартное отклонение выборки.
Решение:
Выборка очевидно не содержит грубых промахов. Рассчитаем среднее арифметическое вариант:
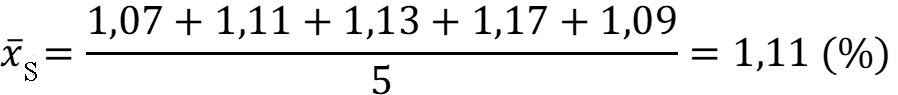
Рассчитаем стандартное отклонение:
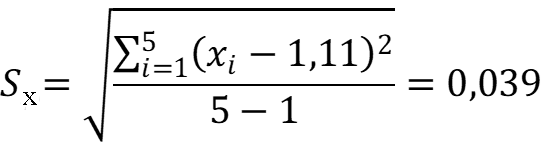
Ответ: ω% (серы) = 1,11 %; Sx = 0,039
Коэффициент вариации или относительное стандартное отклонение.
Оценка разбросанности значений относительно самих значений. В статистике принято, что, если коэффициент вариации меньше 10%, то степень рассеивания данных считается незначительной, от 10% до 20% - средней, больше 20% и меньше или равно 33% - значительной, значение коэффициента вариации не превышает 33%, то совокупность считается однородной, если больше 33%, то – неоднородной.
Относительное стандартное отклонение:

Коэффициент вариации:
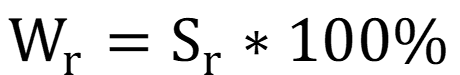
Задача №2:
В образце определяли хлориды рентгенфлуоресцентным методом и методом потенциометрического титрования. Получены следующие результаты (мг/кг):
РФ 12,1 14,1 13,6 14,8 Пт. 13,40 13,75 13,65 13,58
Сравнить воспроизводимости результатов анализа. Возможно ли объединить результаты анализа в одну выборку?
Решение:
Выборки очевидно не содержат грубых промахов. Рассчитаем средние арифметические вариант двух выборок:
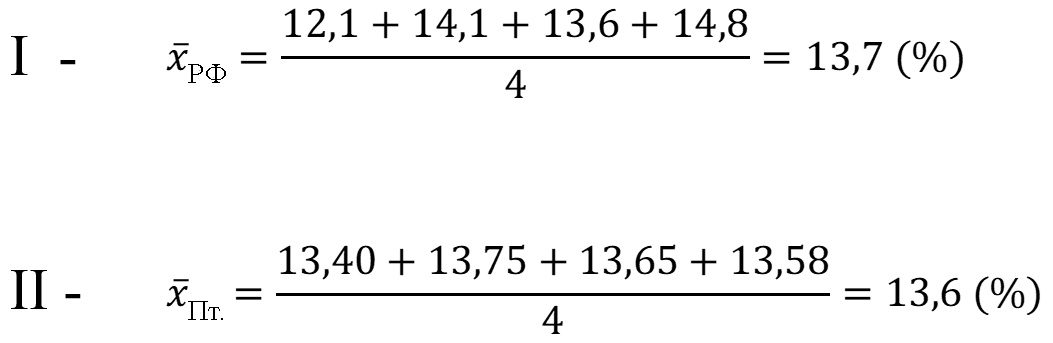
Между средними арифметическими существенного различия нет. Рассчитаем стандартные отклонения выборок:
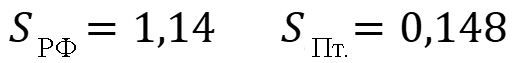
Рассчитаем коэффициенты вариации выборок:
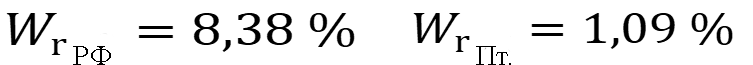
W < 10 % - выборки однородны, но более чем в 7 раз отличаются по воспроизводимости.
Ответ: объединять выборки нельзя.
Видео можно посмотреть тут.

