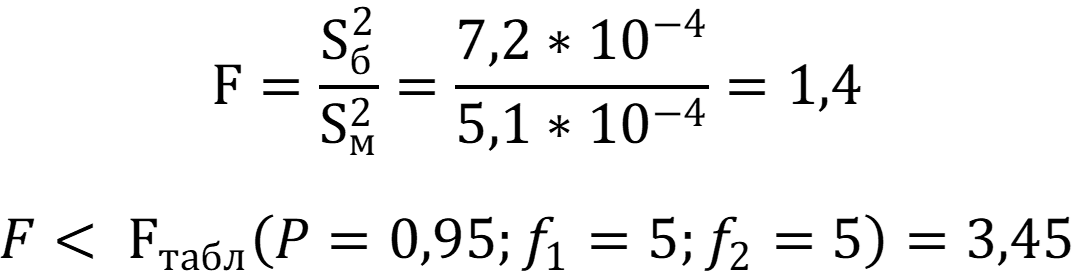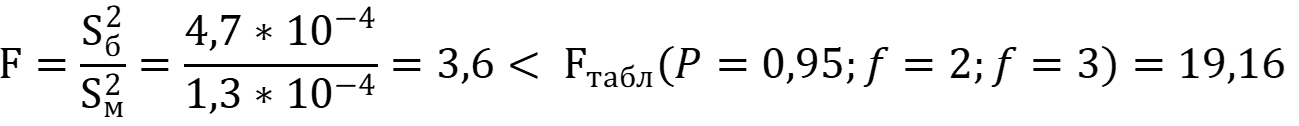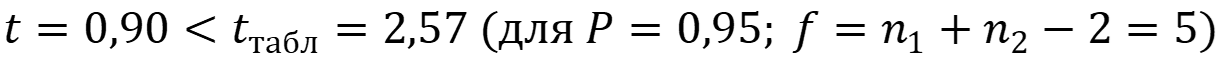АНАЛИТИЧЕСКАЯ ХИМИЯ

Критерий Фишера

При нормальном законе распределения случайных величин используется для проверки гипотезы о различии свойств выборочных дисперсий.

Формула для расчётов:

Найденное значение сравнивается с табличным значением при заданном уровне значимости P и степенях свободы f₁ = n₁ – 1 и f₂ = n₂ - 1. Если F > F_табл. тогда гипотеза о различии в свойствах выборочных дисперсий принимается.

Задача №1:

При определении иодного числа бензиновой фракции различными лаборантами получены данные (г йода на 100 г продукта):

• 10,41; 10,48; 10,41; 10,44; 10,45; 10,45
• 10,48; 10,42; 10,44; 10,43; 10,43; 10,42

Есть ли различия в воспроизводимости двух выборок, возможно ли объединение двух выборок в одну.

Решение:

Выборки очевидно не содержат грубых промахов. Для каждой из выборок рассчитаем средние:

Для каждой из выборок рассчитаем дисперсии по формуле:

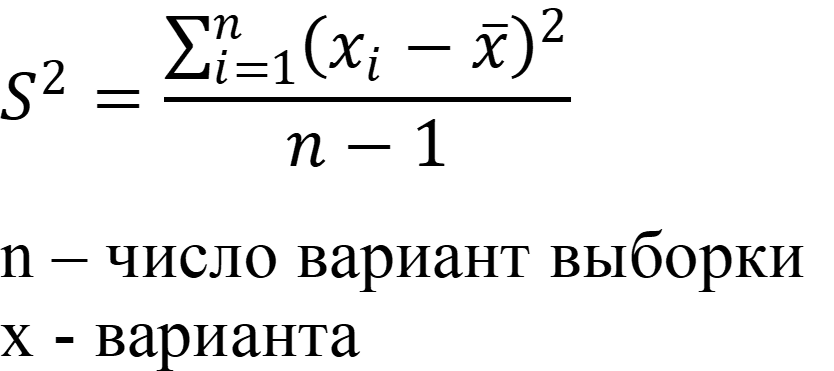
Сравнение дисперсий по критерию Фишера указывает на отсутствие различий в свойствах на уровне значимости 0,95.

Ответ: на уровне значимости 0,95 выборки не различаются по воспроизводимости, средние не отличаются – выборки можно объединить в одну.

Критерий Стьюдента (t – критерий)

Перед применением данного критерия необходимо проверить выборки на однородность по критерию Фишера, также должны отсутствовать грубые промахи.

Разность средних арифметических вариант случайная величина и следует распределению. Величину критерия для двух не зависимых выборок вычисляют по формуле:

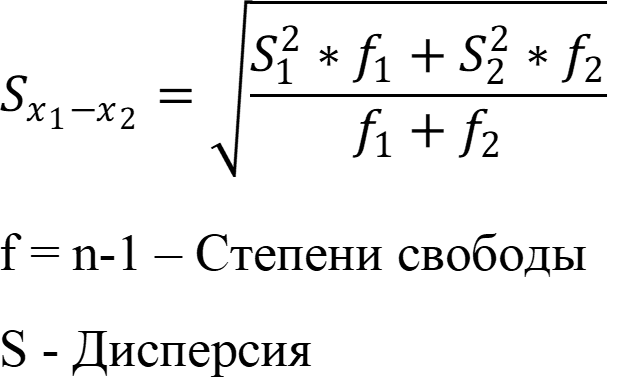
Полученную величину сравнивают с табличным значением, если t < t_табл., то различие между средними считают статистически не значимым.

Задача №2:

При анализе содержания меркаптановой серы в нефти двумя лаборантами получены данные в % масс.:

• 0,45; 0,47; 0,52
• 0,49; 0,50; 0,55; 0,51

Возможно ли объединение двух выборок?

Решение:

Выборки очевидно не содержат грубых промахов. Для каждой из выборок рассчитаем дисперсию по формуле:

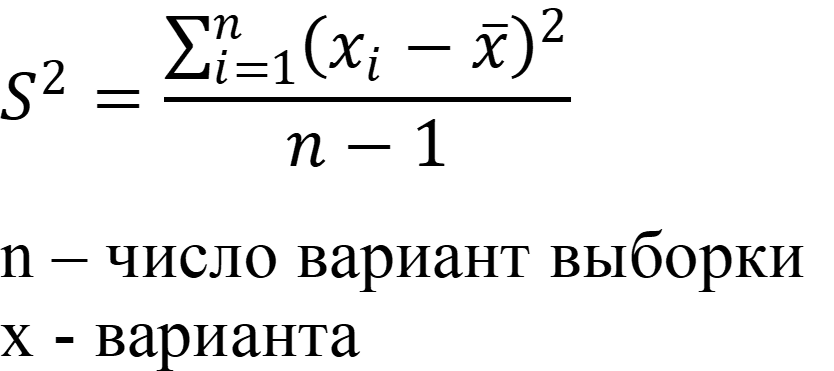
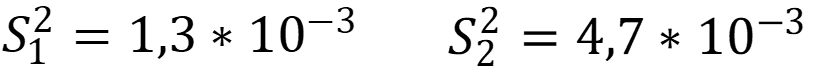
Проверим выборки на однородность по критерию Фишера:

Сравнение дисперсий по критерию Фишера указывает на их однородность на уровне значимости 0,95.

Рассчитаем средние арифметические вариант обоих выборок:

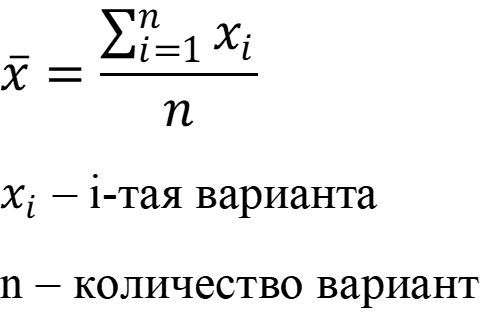
Рассчитаем обобщённую дисперсию двух выборок:

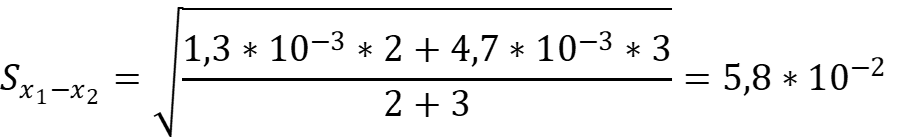
Рассчитаем величину t-критерия:

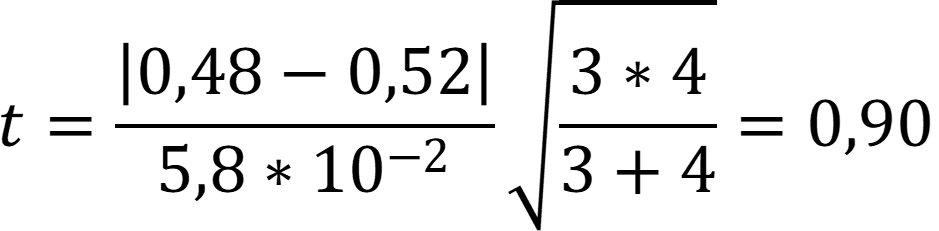
Сравним полученное значение с табличным при заданном уровне значимости:

Так как вычисленное значение меньше табличного, то разница между средними арифметическими вариант статистически не значима.

Ответ: различие статистически не значимо, выборки можно объединить.

Видео можно посмотреть тут.