Метод "введено-найдено"
Метод основан на выявлении введённого точно известного количества добавки искомого компонента проверяемой методикой. Применяется в отсутствии стандартных образцов и методик!
Добавка должна содержать известное количество определяемого компонента, той же форме, что и в анализируемом объекте. Необходимо правильно выбрать размер добавки - должна приводить к достоверному (надежно фиксируемому), но не слишком сильному увеличению аналитического сигнала. Часто рекомендуют вводить такую добавку, чтобы масса искомого компонента в пробе увеличилась на 30–50%.
Метод включает в себя этапы:
- Анализ образца без добавки.
- Анализ образца с добавкой
- Расчёт по разнице количества добавки
- Расчёт доверительного интервала для полученного значения количества добавки
- Сопоставление полученного интервала и точно известного количества добавки m
Если m попадает в границы доверительного интервала, рассчитанного для заданной вероятности, считают, что систематическая погрешность не выявлена, если же m не попадает в границы доверительного интервала, считают, что данная методика содержит значимую систематическую погрешность.
Задача:
При анализе нефтепродукта на содержание неорганического хлора использовали новую методику. Для проверки правильности методики к пробе массой 1 кг добавили 20 мг хлорид ионов и после проведения анализа рассчитывали, на сколько возросла их масса по сравнению с пробами без добавок. Увеличение составило для разных аликвот: 15; 19; 24; 21 и 18 мг/кг. Можно ли с надежностью 0,95 утверждать, что методика имеет значимую систематическую погрешность?
Дано:
mдобавки
= 20 мг/кг
|
|
1 пр. |
2 пр. |
3 пр. |
4 пр. |
5 пр. |
|
Масса добавки, мг/кг |
15 |
19 |
24 |
21 |
18 |
Решение:
Выборка очевидно не содержит грубых промахов. Рассчитаем среднее арифметическое вариант при n = 5:
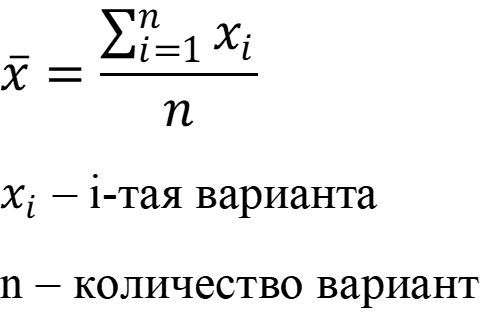
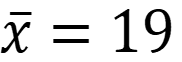
Находим стандартное отклонение:
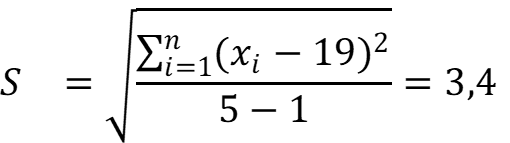
При P = 0,95 и f = n – 1 = 4; t = 2,78
Рассчитаем доверительный интервал:
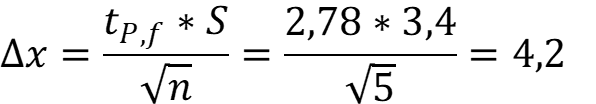
Масса добавки хлорид ионов (19 ± 4) мг/кг. Истинная масса добавки 20 мкг входит в рассчитанный интервал.
Ответ: методика с вероятностью 0,95 не даёт статистически значимых систематических погрешностей.
Видео можно посмотреть тут.

