Метод сравнения с эталоном
Метод основан на применении стандартных образцов с известным химическим составом. Это наиболее надёжный способ!
Стандартные образцы (СО) – это образцы из материала, состав и свойства которого надежно установлены и удостоверены государственным учреждением. Каждый стандартный образец снабжен паспортом, в котором указывается истинное содержание компонента.
Метод включает в себя этапы:
- Анализ стандартного образца проверяемой методикой
- Расчёт статистических характеристик полученных данных (доверительный интервал)
- Сопоставляют паспортное значение содержания (m) с интервалом рассчитанным по полученным данным
Если m попадает в границы доверительного интервала, рассчитанного для заданной вероятности, считают, что систематическая погрешность не выявлена, если же m не попадает в границы доверительного интервала, считают, что данная методика содержит значимую систематическую погрешность.
Следует помнить!
Разумеется, вывод справедлив только для материалов, имеющих примерно тот же состав, что и СО. Необходимо учесть состав примесей, содержание определяемого компонента, форму его существования (степень окисления, закомплексованность и т. п.) и физические свойства материала и образца (одинаково ли их агрегатное состояние, дисперсность). Поэтому для каждого типа анализируемых материалов нужны свои стандартные образцы! Из-за отсутствия необходимых СО многие методики таким способом проверить не удается!
Задача:
Анализ стандартного образца нефти с содержанием 0,40 % по массе воды показал следующие результаты: 0,38; 0,34; 0,35. Существует ли статистически значимая систематическая погрешность при определении по данной методике?
Дано:
Вещество 1
опр. 2
опр. 3
опр. Содержание Вода, %
масс. 0,38 0,34 0,35 0,40
Решение:
Выборка не содержит грубых промахов. Рассчитаем среднее арифметическое вариант при n = 3:
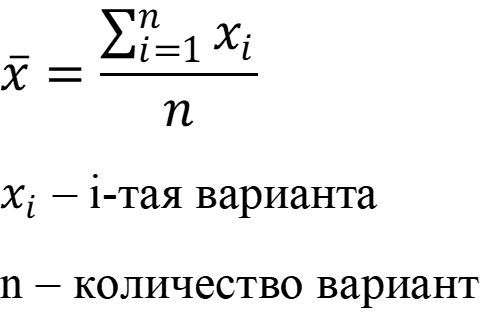
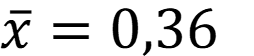
Находим стандартное отклонение:
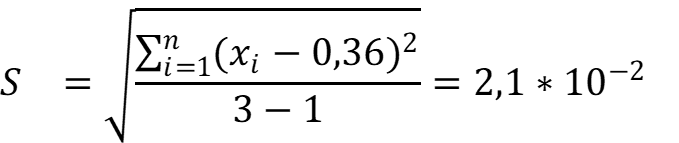
При P = 0,95 и f = n – 1 = 2; t = 4,30.
Рассчитаем доверительный интервал:
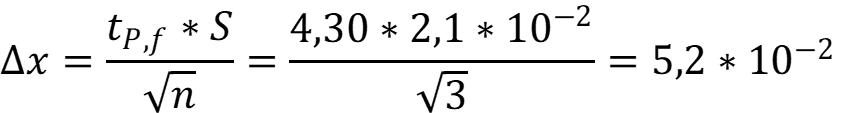
Содержание воды (0,36 ± 0,05) %. Содержание из паспорта входит в интервал рассчитанный по данным полученным методикой.
Ответ: методика с вероятностью 0,95 не даёт статистически значимых систематических погрешностей.
Видео можно посмотреть тут.

