Расчёт состава раствора [47]

Для описания сложных систем кроме уравнений, связывающих концентрации и константы ионизации, используются уравнения материального баланса и электронейтральности.

  • Уравнение материального баланса. Число атомов данного типа в изолированной системе неизменно (закон сохранения массы). Например, известно, что при образовании раствора угольной кислоты и воды (задаваемая при приготовлении общая концентрация кислоты Co) в растворе (при каком-то определенном рН) могут находиться следующие частицы: H2CO3, HCO3-, CO32-, H3O+, OH−.
    Балансовое уравнение по аниону кислоты будет иметь вид:
    Co = [H2CO3] + [HCO3-] + [CO32-].
  • Условие электронейтральности соблюдается для любого электролита: суммарный заряд гомогенной жидкой системы, содержащий диссоциированный электролит, равен нулю, т.е. общее число положительных зарядов равно общему числу отрицательных зарядов.
    Например, для водного раствора Ca(HCO3)2, в котором находятся ионы Ca2+, HCO3-, CO32-, H3O+, OH−, уравнение электронейтральности имеет вид:
    2[Ca2+] - [HCO3-] - 2[CO32-] + [H3O+] + [OH−] = 0.
Ионные равновесия в растворах двухосновных слабых кислот и оснований

В водном растворе слабой двухосновной кислоты/основания возможно протекание следующих линейно независимых реакций: реакции автопротолиза воды и реакции ионизации слабой кислоты/основания по двум ступеням.

Задача №1:

Имеется водный раствор адипиновой кислоты, концентрация которой 0,01 моль/л. Справочные данные: Ka1 = 3,9 * 10−5, Ka2 = 5,1 * 10−6, Kw = 1,0 * 10-14. Найти концентрации всех ионов в данном растворе.

Дано:

Ka1 = 3,9 * 10−5
Ka2 = 5,1 * 10−6
Kw = 1,0 * 10-14
Cобщ. = 0,01 моль/л
[H3O+], [(CH2)4(COOH)2], [(CH2)4(COOH)COO-], [(CH2)4COO22-] - ?

Решение:

В водном растворе адипиновой кислоты протекают следующие реакции, характеризующиеся глубиной протекания x:
H2O + H2O ↔ H3O+ + OH-,                                                      x1
(CH2)4(COOH)2 + H2O ↔ H3O+ + (CH2)4(COOH)COO-,      x2
(CH2)4(COOH)COO- + H2O ↔ H3O+ + (CH2)4(COO)22-        x3

Равновесие описывается системой уравнений:

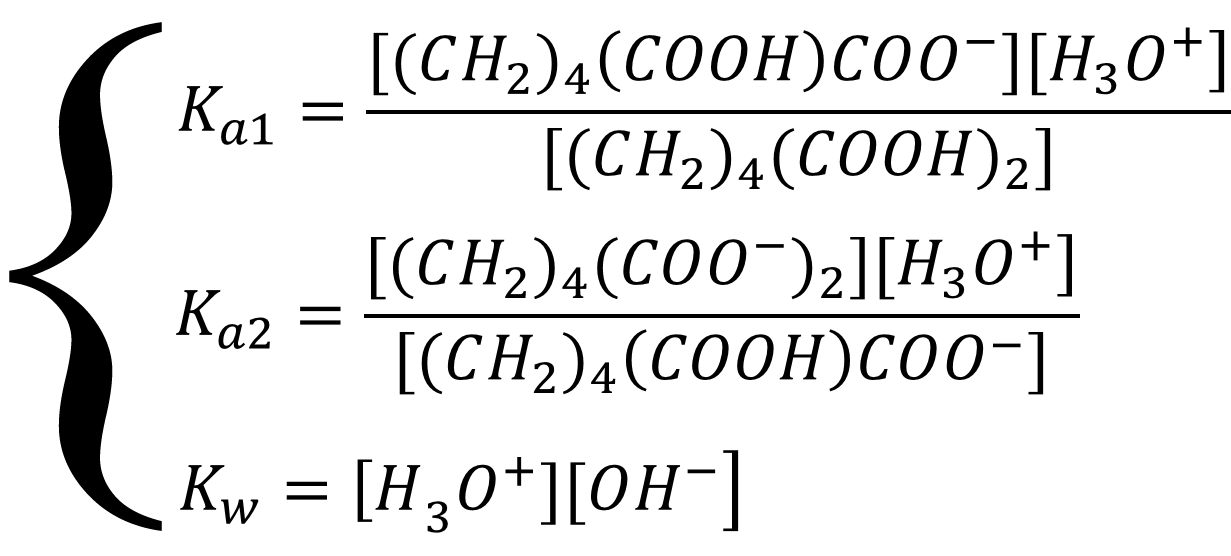
dvuhosnk-ta.png

Выразим все равновесные концентрации через глубины протекания трёх реакций: [H3O+] = x1 + x2 + x3; [OH-] = x1; [(CH2)4(COOH)COO-] = x2 - x3; [(CH2)4(COO)22-] = x3; [(CH2)4(COOH)2] = Cобщ - x2 и подставим в систему уравнений:

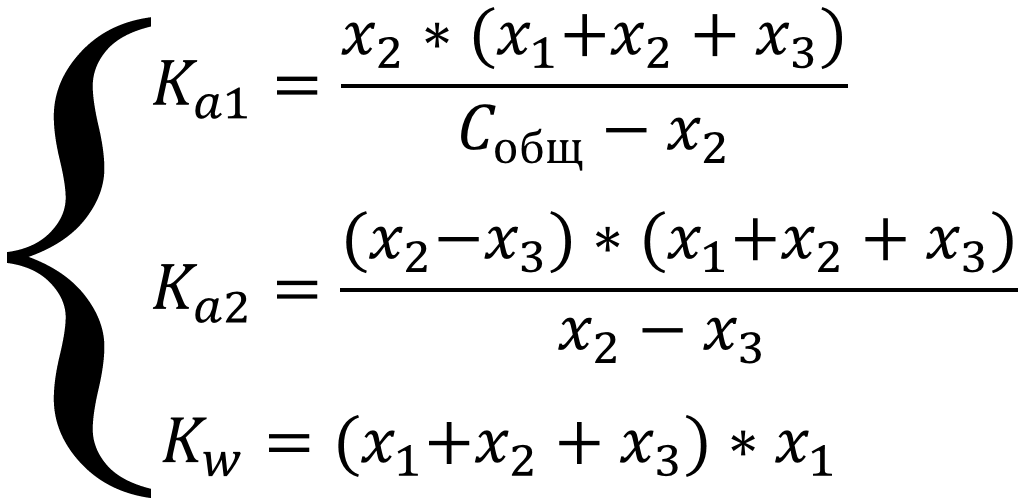
dvuhosnk-ta1.png

Систему можно упростить, если в уравнениях там, где стоит алгебраическая сумма, пренебречь меньшими слагаемыми из уравнения автопротолиза x1 и слагаемым x3, так как вторая ступень диссоциации подавляется ионами водорода выделяющимися при диссоциации по первой ступени, т.е. x1 и x3 << x2, тогда уравнения примут вид:

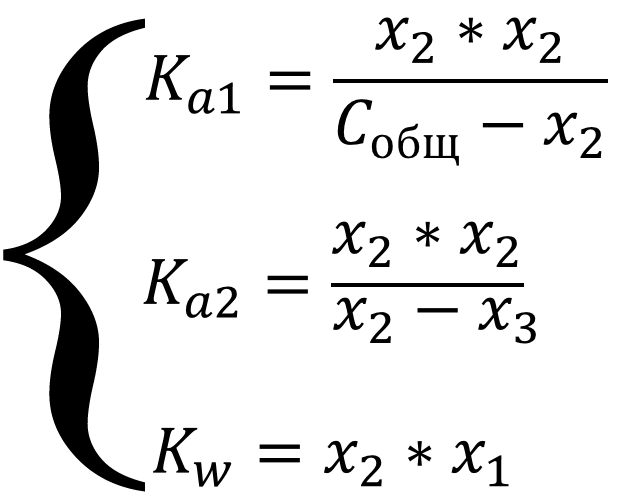
dvuhosnk-ta2.png

Выражение для первой константы кислотности имеет вид обычного квадратного уравнения, рассчитаем сначала x2, а потом x1 и x3 из выражения для константы автопротолиза и второй ступени ионизации кислоты:

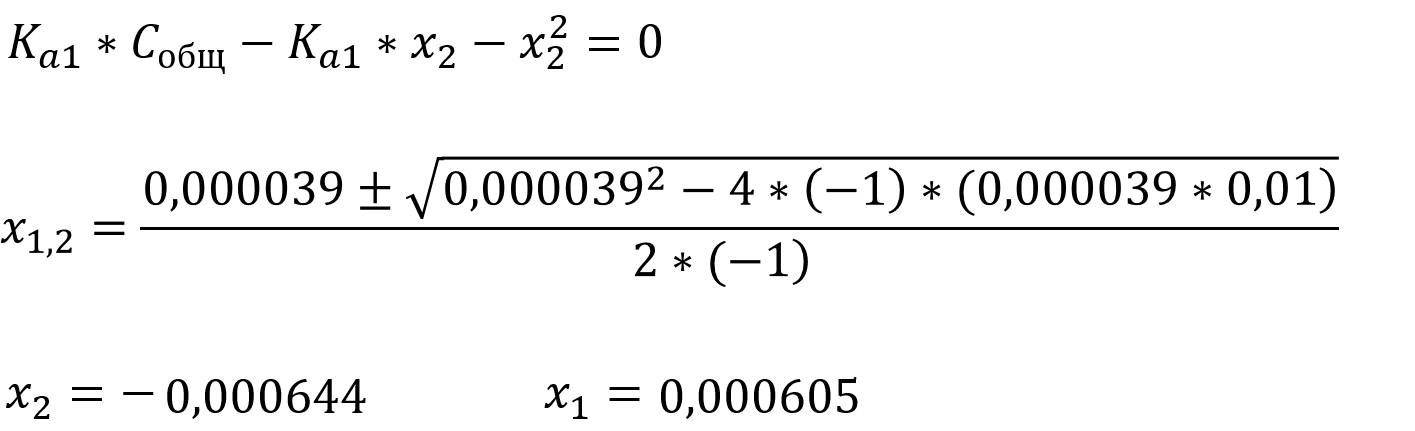
dvuhosnk-ta3.png

Так как мы ищем концентрацию, которая не может быть отрицательной, то верным считается положительный корень уравнения, соответственно:

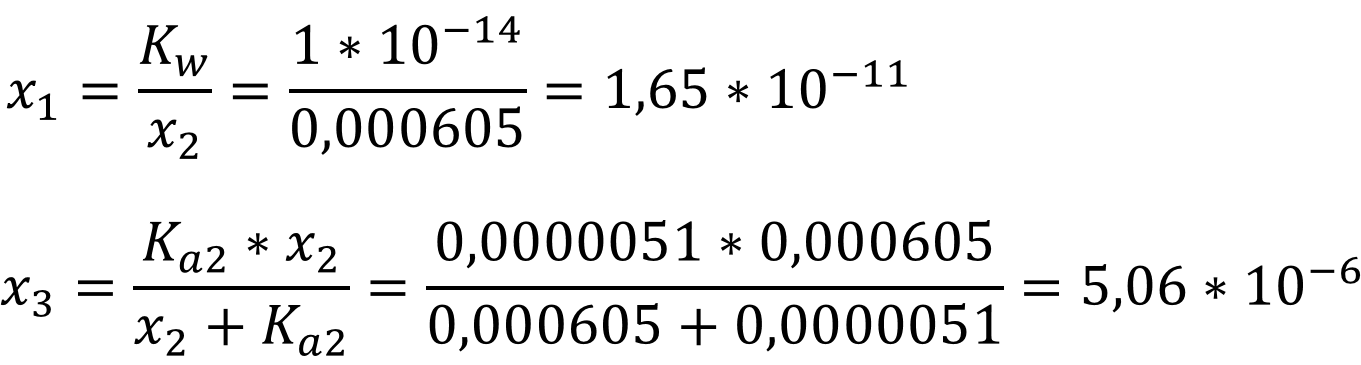
dvuhosnk-ta4.png

Из исходных уравнений рассчитаем концентрации ионов входящих в раствор:
[H3O+] = x1 + x2 + x3 = 0,00061 моль/л;
pH = -lg[H3O+] = 3,21;
[OH-] = x1 = 1,65 * 10−11 моль/л;
[(CH2)4(COOH)COO-] = x2 - x3 = 0,00060 моль/л;
[(CH2)4(COO)22-] = x3 = 5,06 * 10-6 моль/л;
[(CH2)4(COOH)2] = Cобщ - x2 = 0,01 - 0,000605 = 0,0094 моль/л.

Ответ: [H3O+] = 0,00061 моль/л;
pH = -lg[H3O+] = 3,21;
[OH-] = 1,65 * 10−11 моль/л;
[(CH2)4(COOH)COO-] = 0,00060 моль/л;
[(CH2)4(COO)22-] = 5,06 * 10-6 моль/л;
[(CH2)4(COOH)2] = 0,0094 моль/л.
Полученный результат показывает, что сделанное ранее допущение о том, что x1 и x3 << x2, верное. При анализе сложных систем всегда стоит учитывать значимость тех или иных процессов, для последующего упрощения системы уравнений!!!

Задача №2:

Рассчитать концентрации всех ионов в 0,01 М растворе гидразина. Справочные данные: Kb1 = 9,33 * 10−7, Kb2 = 1,86 * 10−14, Kw = 1,0 * 10-14.

Дано:

Kb1 = 9,33 * 10−7
Kb2 = 1,86 * 10−14
Kw = 1,0 * 10-14
Cобщ. = 0,01 моль/л
[OH-], [N2H5+], [N2H62+] - ?

Решение:

В водном растворе слабого основания гидразина протекают следующие реакции, характеризующиеся глубиной протекания x:
H2O + H2O ↔ H3O+ + OH-,         x1
N2H4 + H2O ↔ OH- + N2H5+,      x2
N2H5+ + H2O ↔ OH- + N2H62+    x3

Равновесие описывается системой уравнений:

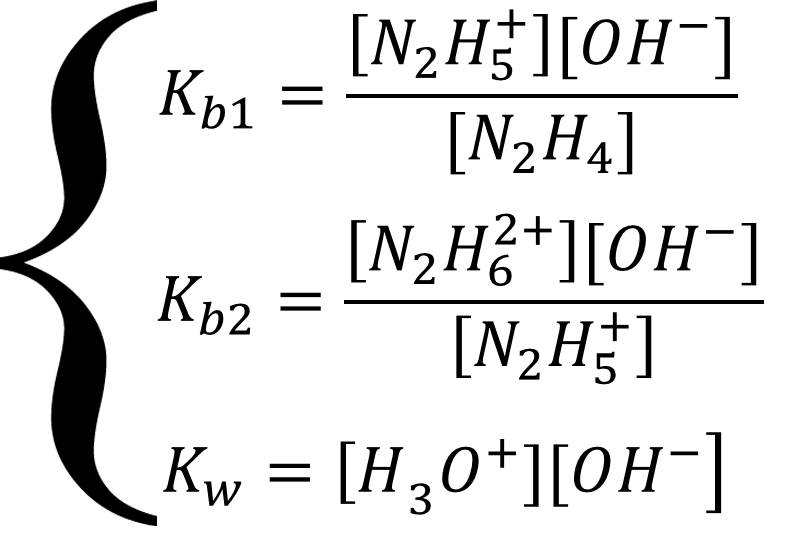
dvuhosnosn.png

Выразим все равновесные концентрации через глубины протекания двух реакций: [OH-] = x1 + x2 + x3; [H3O+] = x1; [N2H5+] = x2 - x3; [N2H62+] = x3; [N2H4] = Cобщ - x2 и подставим в систему уравнений:

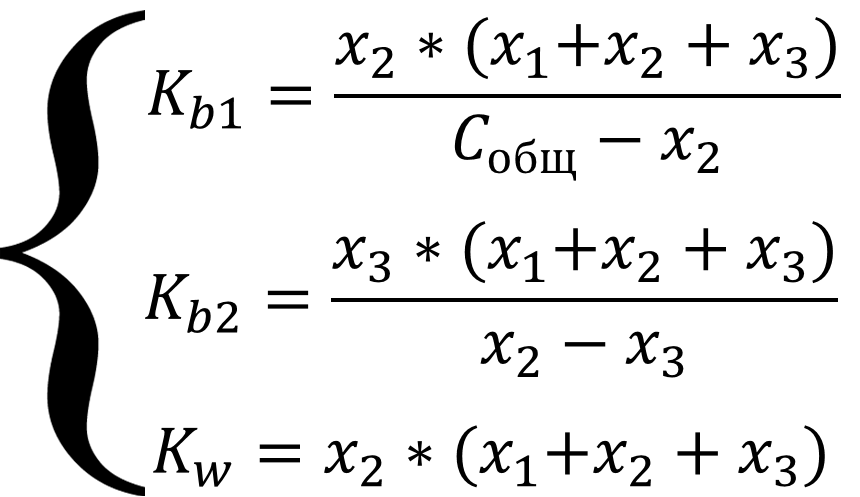
dvuhosnosn1.png

Систему можно упростить, если в уравнениях там, где стоит алгебраическая сумма, пренебречь меньшими слагаемыми из уравнения автопротолиза x1 и слагаемым x3, так как вторая ступень диссоциации подавляется гидроксил-ионами выделяющимися при диссоциации по первой ступени, т.е. x1 и x3 << x2, тогда уравнения примут вид:

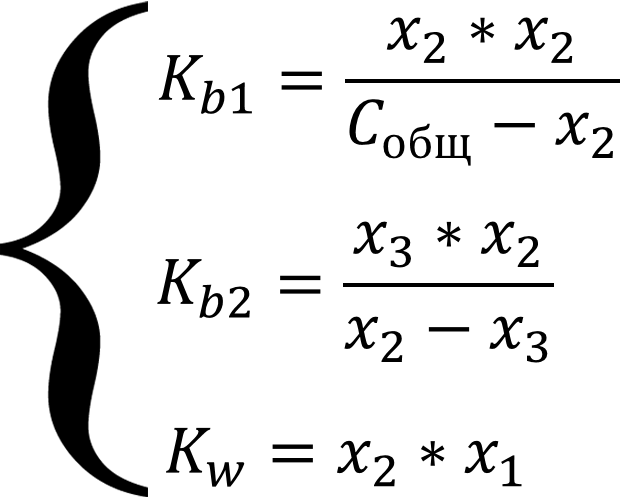
dvuhosnosn2.png

Выражение для первой константы кислотности имеет вид обычного квадратного уравнения, рассчитаем сначала x2, а потом x1 и x3 из выражения для константы автопротолиза и второй ступени ионизации основания:

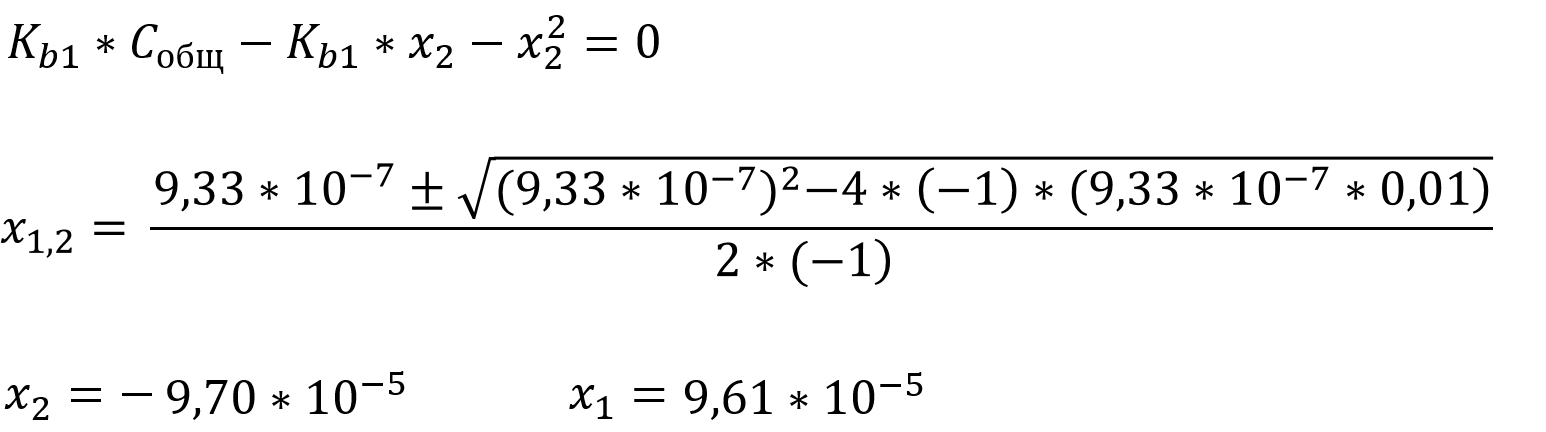
dvuhosnosn3.png

Так как мы ищем концентрацию, которая не может быть отрицательной, то верным считается положительный корень уравнения, соответственно:

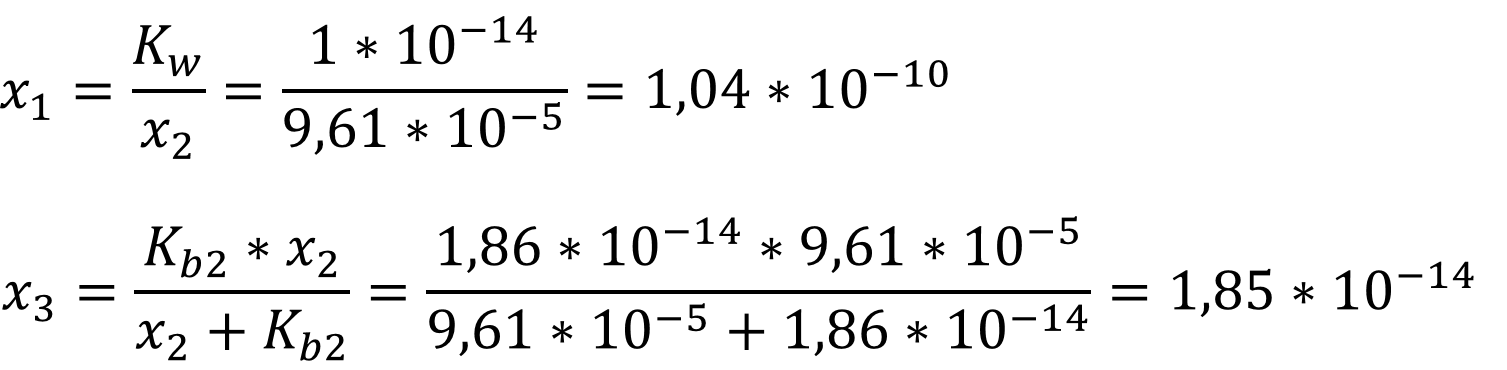
dvuhosnosn4.png

Из исходных уравнений рассчитаем концентрации ионов входящих в раствор:
[OH-] = x1 + x2 + x3 = 0,0000961 моль/л;
pH = 14 + lg[OH-] = 9,98;
[H3O+] = x1 = 1,04 * 10−10 моль/л;
[N2H5+] = x2 - x3 = 0,0000961 моль/л;
[N2H62+] = x3 = 1,85 * 10-14моль/л;
[N2H4] = Cобщ - x2 = 0,01 - 0,0000961 = 0,0099 моль/л.

Ответ: [OH-] = 0,0000961 моль/л;
[H3O+] = 1,04 * 10−10 моль/л;
[N2H5+] = 0,0000961 моль/л;
[N2H62+] = 1,85 * 10-14моль/л;
[N2H4] = 0,0099 моль/л.

Распределительные диаграммы для двухосновных кислот/оснований

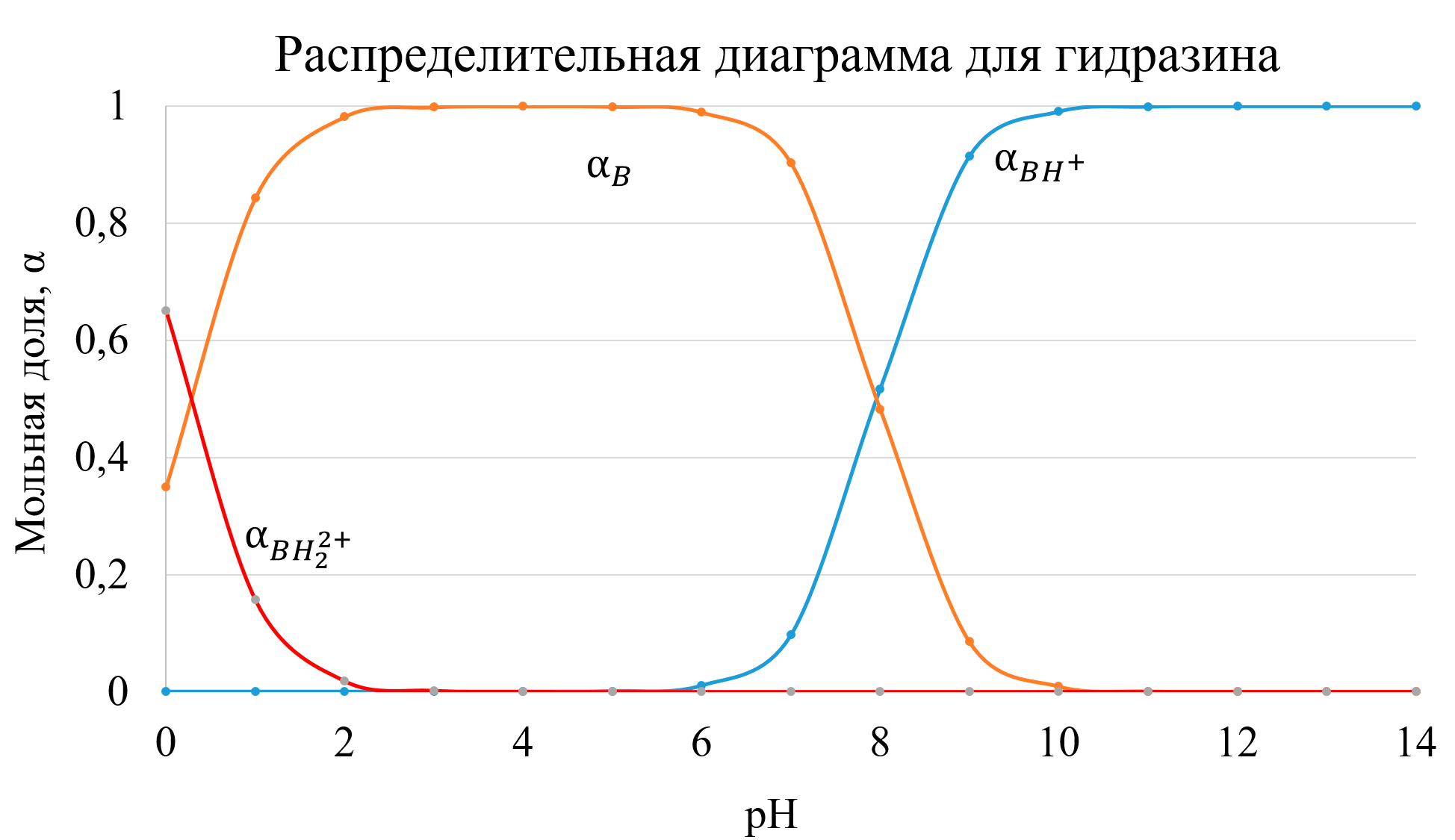
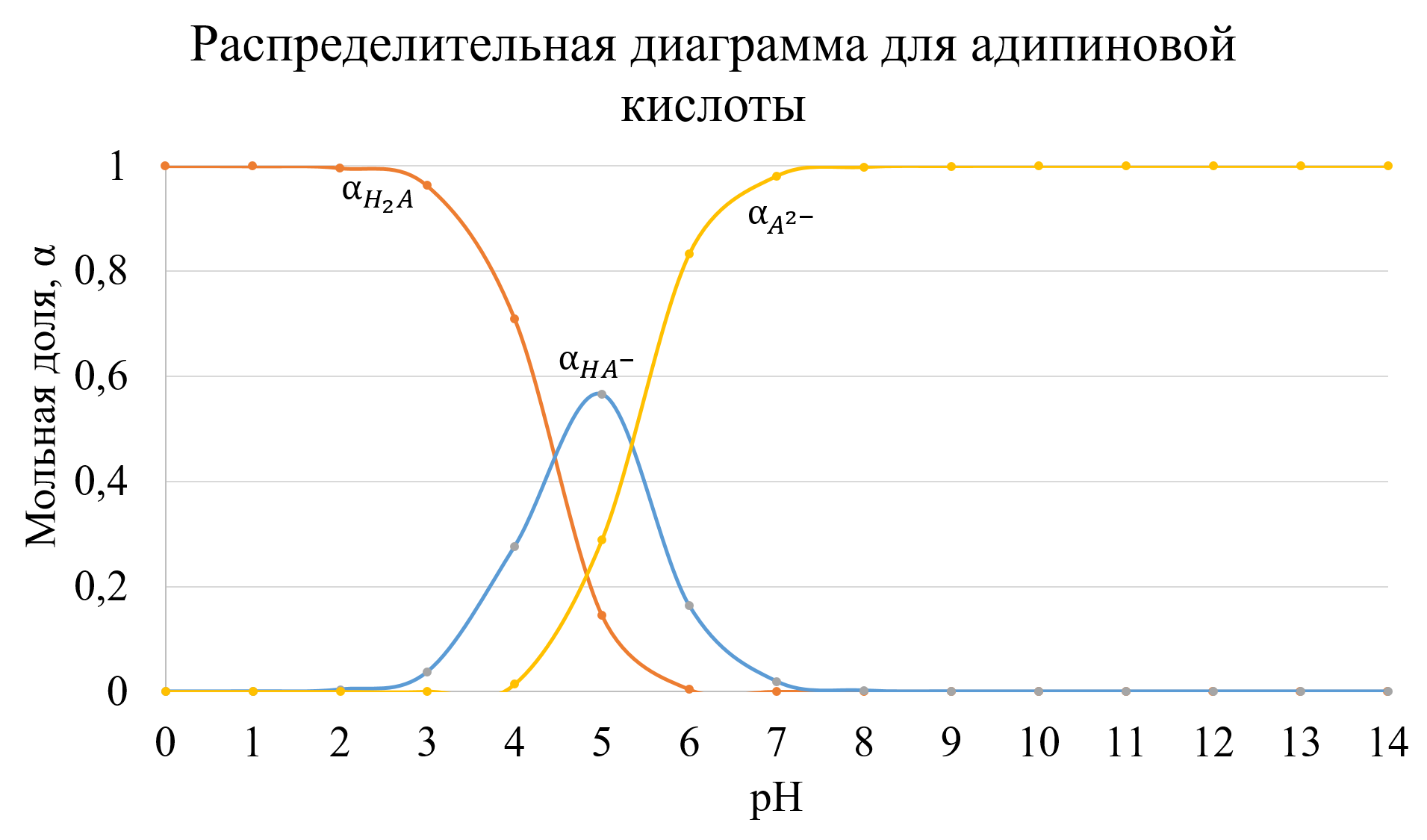
Распределительная диаграмма − это графический образ, позволяющий оценить распределение различных возможных форм какого−либо соединения в зависимости от определенного параметра. Обычно изображают графические зависимости долевых концентраций различных форм от величины pH (все формы на одном графике) и получают таким образом распределительную диаграмму. При построении распределительных диаграмм делают допущения:

  • пренебрегают вкладом реакции автопротолиза воды в общий процесс;
  • принимают активности ионных форм равными их концентрациям, т.е. пренебрегают силами взаимодействия между ионами, молекулами.

Мольная доля − это отношение равновесной концентрации данного иона к общей концентрации всех форм ионов. После упрощения для двухосновной кислоты имеем:

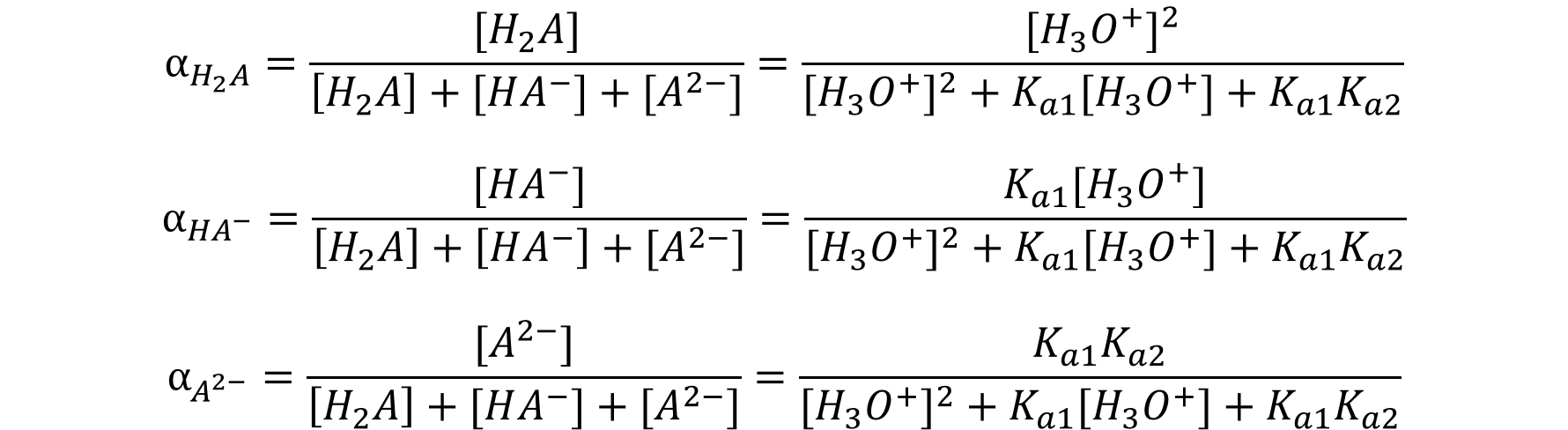
mddosnk.png

Для адипиновой кислоты с Ka1 = 3,9 * 10-5 и Ka2 = 5,1 * 10-6 диаграмма имеет вид:

mddosnk1.png

Упрощение для одноосновного основания даёт:

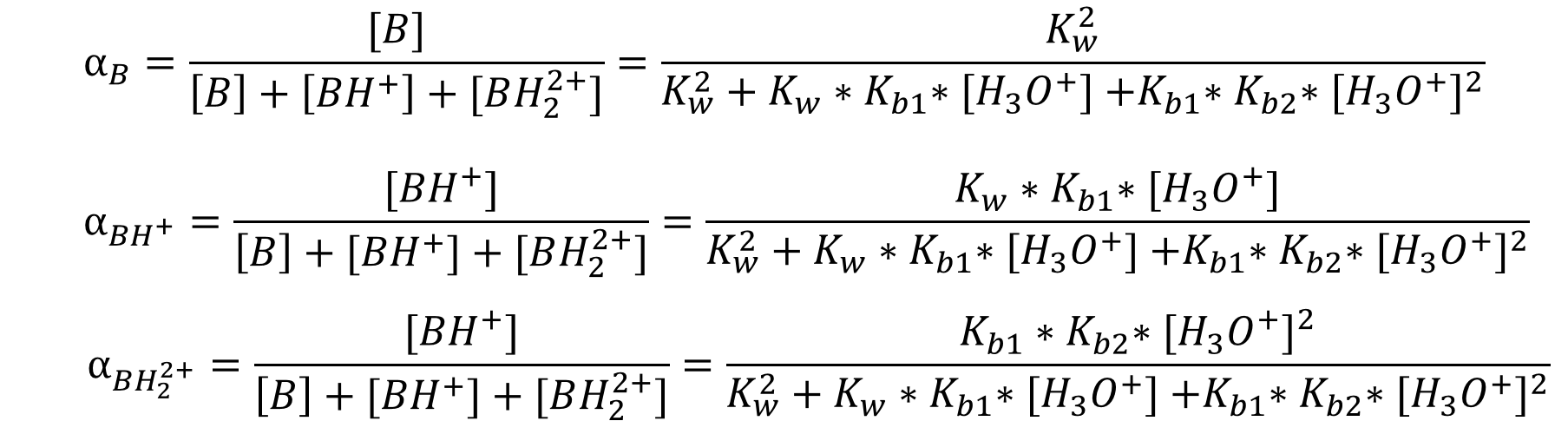
mddosno.png

Для диэтиламина с Kb1 = 9,33 * 10−7 и Kb2 = 1,86 * 10−14 диаграмма имеет вид:

mddosno1.png