Выявление дрейфа данных
Дрейф подразумевает под собой монотонное возрастание или убывание измеряемой величины, обычно это связано с изменением состава пробы или реагентов во времени.
При наличии дрейфа данных дальнейшая статистическая обработка невозможна. Для выявления дрейфа необходимо иметь от 5 вариант в выборке, каждая из которых больше или меньше предъидущей. При этом используют сравнение средних арифметических вариант двух равных частей выборки по t – критерию, предварительно отбраковав грубые промахи.
Парный критерий Стьюдента (t – критерий)
Разность средних арифметических вариант случайная величина и следует t – распределению.
Величину критерия вычисляют по формуле:

Полученную величину сравнивают с табличным значением, если t < tтабл., то различие между средними считают не значимым, а наличие дрейфа данных недоказанным на заданном уровне P.
Задача:
При анализе содержания СО2 в воздухе промышленного помещения получены данные в % масс.: 0,45; 0,47; 0,49; 0,50; 0,52; 0,55; 0,56. Проверить данные на наличие дрейфа. Возможна ли дальнейшая работа с данными?
Решение:
Выборка не вызывает подозрений о наличии грубых промахов. разделим выборку на равные части:
- 0,45; 0,47; 0,49 n = 3
- 0,50; 0,52; 0,55; 0,56 n = 4
Рассчитаем средние арифметические вариант обоих выборок:

Рассчитаем величину t – критерия:
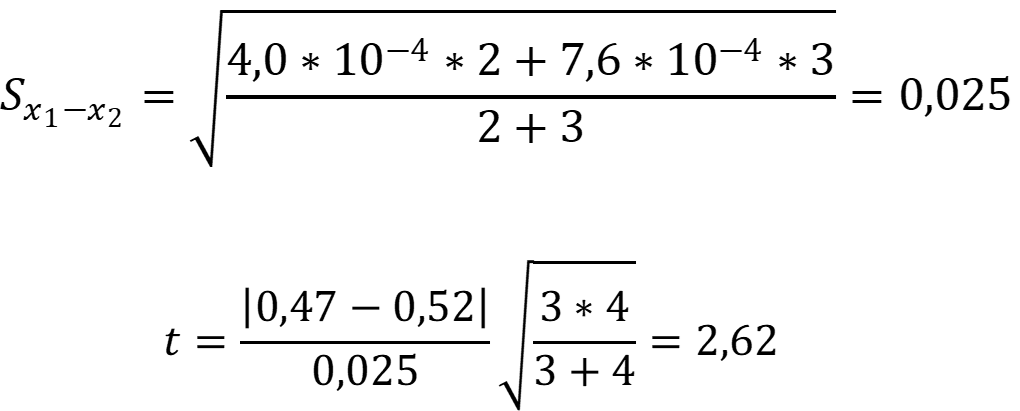
Сравним полученное значение с табличным при заданном уровне значимости:
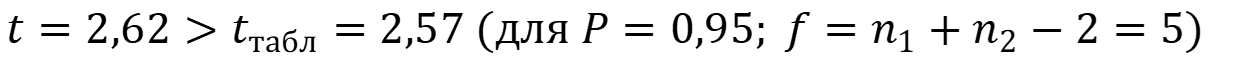
Так как вычисленное значение больше табличного, то разница между средними арифметическими вариант статистически значима.
Ответ: Наличие дрейфа данных доказано на уровне значимости Р = 0,95 дальнейшая работа с данными методами статистической обработки невозможна.
Видео можно просмотреть тут.

