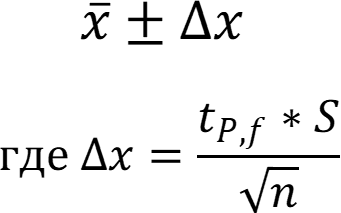АНАЛИТИЧЕСКАЯ ХИМИЯ

Получаемые при аналитических измерениях числа являются приближенными значениями измеряемых физических величин, так как содержат в себе некоторую погрешность определения.

Таким образом, цель исследователя: по малой выборке из нескольких случайных определений оценить центральное значение определяемой величины, а также то, в какой интервал (с заданной надежностью) могут укладываться наиболее вероятные результаты анализа данного образца. Если в методике анализа отсутствует систематическая погрешность, истинное значение содержания аналита будет находиться внутри этого интервала.

Результат анализа представляется в виде:

где t_P,f – коэффициент Стьюдента для доверительной вероятности Р и числа степеней свободы f;

S – абсолютное стандартное отклонение измеряемой величины, рассчитанное для выборки из n данных.

Задача:

При определении содержания свинца фотометрическим методом с дитизоном в сточных водах после исключения промахов были получены следующие результаты (мг/дм³): 0,014; 0,017; 0,015; 0,015; 0,016; 0,018; 0,015; 0,016; 0,014. Рассчитать содержание свинца в воде.

Решение:

Выборка очевидно не содержит грубых промахов. Рассчитаем среднее арифметическое вариант при n = 9:

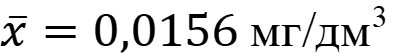
Находим стандартное отклонение:

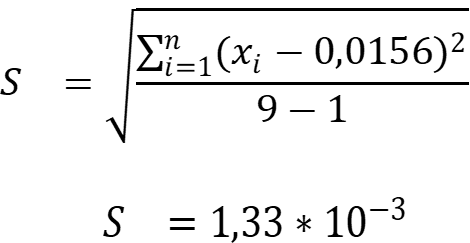
При P = 0,95 и f = 9 – 1 = 8; t = 2,31.

Рассчитаем доверительный интервал:

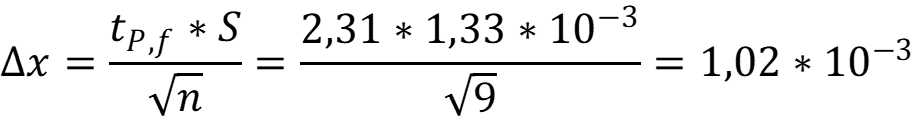
Результат записывается с точностью до порядка ограничиваемого доверительным порядком, значение доверительного интервала записывается с одной значащей цифрой.

Ответ: Содержание Pb (0,015±0,001) мг/дм³.

Видео можно посмотреть тут.